Wersja video
Jesli wolisz oglądać niż czytać, obejrzyj film o tym, czy matma jest łatwa.
Wersja tekstowa
Powiem przewrotnie: tak, matma jest łatwa!
No weź Alicja, jak matma może być łatwa?
Tak, wiem, jak to brzmi… Matma łatwa?! Już tłumaczę…
Spójrz na poniższe działania.
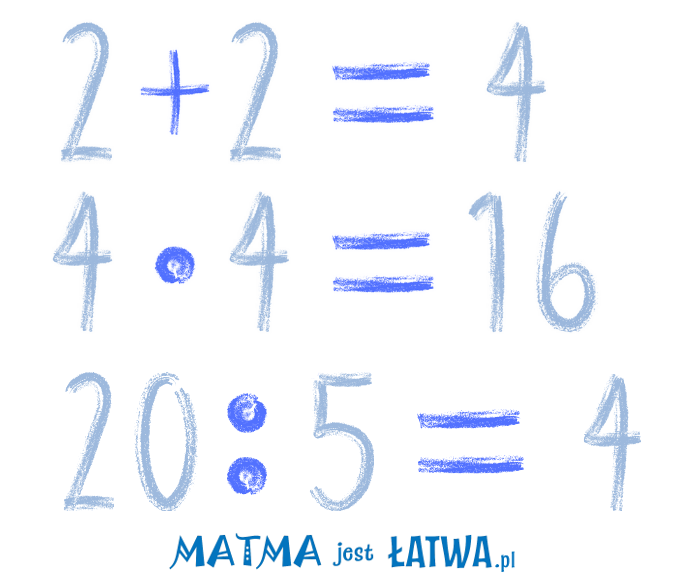
Wiesz skąd się wzięły wyniki, prawda? No tak, przecież to łatwe :) A skąd to wiesz? Z podstawówki, prawda? Ktoś cię nauczył dodawania, mnożenia i dzielenia przez proste liczby.
Wiesz skąd się wzięły wyniki, prawda? No tak, przecież to łatwe :) A skąd to wiesz? Z podstawówki, prawda? Ktoś cię nauczył dodawania, mnożenia i dzielenia przez proste liczby.
’Trudniejszych’ działań też możesz się nauczyć. Tak, są one bardziej skomplikowane, ale wcale nie trudniejsze. Po prostu trzeba im poświęcić więcej czasu. I więcej ćwiczeń.
Skąd zatem wynikają trudności i problemy z matmą? Wcale nie z tego, że ktoś jest matematycznym głąbem. Nie, nie, nie!
Po prostu i zwyczajnie na bardziej skomplikowane matematyczne tematy trzeba poświęcić więcej czasu. Rzadko zdarzają się osoby, które załapią taki temat od razu na lekcji i to wystarczy. Najczęściej trzeba w domu usiąść i do tematu wrócić, a przede wszystkim spróbować policzyć więcej przykładowych zadań niż na lekcji.
Na lekcji nauczyciel często nie ma czasu aby skupić się na temacie na tyle dogłębnie (i przeliczyć tyle zadań), żeby każdy uczeń go zrozumiał. Niektórzy uczniowie zrozumieją w lot, ale takich osób jest mniejszość. Większość będzie potrzebowała więcej czasu i przeliczonych zadań aby dany temat zrozumieć.
A wszystkie te tematy będą potrzebne na egzaminie ósmoklasisty, a później na maturze.
Pokażę ci to na przykładzie. Oblicz takie pierwiastki:
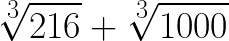
Większość osób chwyci się w tym momencie za głowę i popatrzy bezradnie. Jak się za to w ogóle zabrać? Wydaje się trudne i nie do przejścia. Chyba, że policzysz na kalkulatorze, ale nie o to tu chodzi. Spróbuj zrobić to zadanie ze mną ręcznie.
Pokażę ci, że wystarczy, aby ktoś we właściwy sposób wytłumaczył ci jak takie zadanie z pierwiastkami trzeciego stopnia zrobić, a zrozumiesz. i następne takie zadanie zrobisz sam. a trzecie to już w ogóle będzie pikuś ;)
Zabierzmy się najpierw za pierwszy pierwiastek. Nie wygląda to na pierwszy rzut oka sympatycznie, prawda?
Gdyby był to pierwiastek drugiego stopnia, to byłoby zdecydowanie łatwiej. Wystarczyłoby zauważyć, że liczba 216 dzieli się fajnie przez 4:
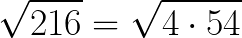
A dalej, 54 dzili się przez 9:
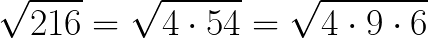
Ponieważ pod pierwiastkiem mamy mnożenie, możemy więc rozbić go na trzy pierwiastki:
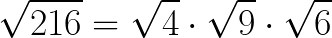
Z czwórki i dziewiątki możemy pierwiastek wyciągnąć. Pierwiastek szóstki byłby nieładnym ułamkiem, a więc zostawiamy szóstkę pod znakiem pierwiastka:
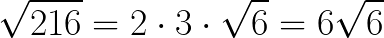
I voila – mamy gotowy wynik. Czy jest to dla ciebie zrozumiałe, jak obliczyliśmy pierwiastek drugiego stopnia z 216?
Cóż zatem zrobić, aby policzyć pierwiastek trzeciego stopnia z liczby 216?
Zauważ, że aby dostać ładny wynik z obliczenia pierwiastka drugiego stopnia, pod pierwiastkiem tym potrzebujemy mieć dwie takie same liczby pomnożone przez siebie:

Albo:

Albo:
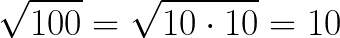
Analogicznie, jeśli mamy pierwiastek trzeciego stopnia, pod pierwiastkiem tym potrzebujemy mieć TRZY takie same liczby pomnożone przez siebie, na przykład:
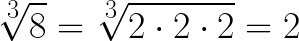
Albo:

Widzisz już co to jest pierwiastek trzeciego stopnia?
Ale Alicja, ja w ogóle nie widzę jak ten pierwiastek wyciągnąć z 216! Ano tak, bo a taką większą liczbą trzeba pobawić się trochę dłużej. Najlepiej rozbić ją sobie na czynniki pierwsze. Jak rołożyć liczbę na czynniki pierwsze pisałam tu, więc nie będę już powtarzała całego wywodu. Wypiszmy sobie zatem wszystkie jak najmniejsze liczby, przez które dzieli się 216:

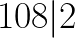
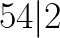
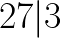
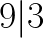
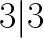
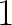
A więc nasza liczba 216 ma następujące dzielniki:
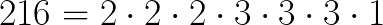
Możemy to samo zapisać również pod naszym pierwiastkiem:
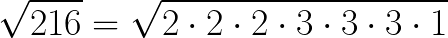
Pod pierwiastkiem mamy zatem trzy dwójki i trzy trójki pomnożone przez siebie. A więc możemy łatwo wyciągnąć pierwiastek trzeciego stopnia z naszej liczby:
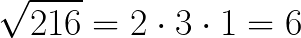
Pierwiastek dowolnego stopnia z jedynki zawsze będzie wynosił 1, bo:
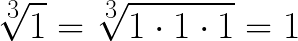
I tak samo z tysiaka:

Wracamy do naszego zadania, które teraz łatwo już policzymy:
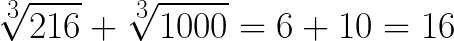
Czy nadal uważasz, że to zadanie jest trudne? ;) Owszem, wymagało trochę zabawy, czasu i uwagi oraz skupienia się na liczeniu. Ale już rozumiesz skąd się co wzięło, prawda? Jeśli nie, zapytaj w komentarzu. Tak czy siak, to piona dla ciebie za poświęcony czas i za przebrnięcie ze mną przez meandry pierwiastków!

Tak samo możemy przebrnąć przez każdy matematyczny temat. Od tematów całkiem podstawowych, po te bardziej i najbardziej zaawansowane, których niektórzy będą uczyli się na studiach.
Matma to konkret i za to tak bardzo ją lubię. Jeśli znasz metodę, wykorzystasz wzór albo triki, których też uczę na moich lekcjach, to poradzisz sobie z nią coraz lepiej i lepiej. Aż w końcu być może ją polubisz! :)