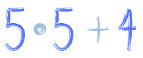O co w ogóle chodzi z tym rozkładaniem liczby na czynniki pierwsze? Co to znaczy?
Wersja video
Obejrzyj film jak rozłożyć liczbę na czynniki pierwsze
Wersja tekstowa
Rozłożenie liczby na czynniki pierwsze to znalezienie wszystkich jej dzielników. A co to jest dzielnik? Dzielnik liczby X to taka całkowita liczba Y, przez którą liczba X dzieli się bez reszty.
Prościej będzie gdy pokażę ci to na przykładzie.
Weźmy na początek łatwą liczbę 2. Przez jakie liczby dzieli się 2? Pewnie powiesz, że przez 2. No i przez 1, prawda? A więc dzielnikami liczby 2 są liczby 2 i 1.
Weźmy liczbę 4. Przez co dzieli się 4? Na pewno przez 4, no i przez 2. Chwila, chwila, ale też przez 1. Przy rozkładaniu liczby na czynniki pierwsze pomija się ową największą liczbę, czyli w tym przypadku 4. Po prostu w praktyce do niczego się ona nie przydaje. No i każdy przecież wie, że 2 dzieli się przez 2, a 333 dzieli się przez 333, no nie? A więc dzielnikami liczby 4 są liczby 4, 2 i 1.
Jak rozłożyć na czynniki pierwsze liczbę 45?
Żeby nie było zbyt łatwo, weźmy większe liczby.
Na pierwszy ogień leci 45. Wypiszemy wszystkie dzielniki liczby 45, w kolejności od największej liczby pierwszej, przez którą się 45 dzieli. W kolejce puka do nas 5, prawda? A więc piszemy:
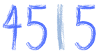
Gdy podzielimy 45 przez 5, dostajemy co? 9, prawda? Wynik dzielenia piszemy poniżej liczby 45:
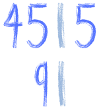
Gdy podzielimy 45 przez 5, dostajemy co? 9Teraz myślimy przez co dzieli się 9. Od razu przychodzi nam do głowy 3. A więc mamy już:

Dzielimy teraz owo 9 przez 3 i dostajemy 3. I znów, wynik dzielenia piszemy pod liczbą wyjściową, czyli pod 9:

A 3 dzieli się przez co? Przez 3, prawda? Wynik tego dzielenia znów zapiszemy z prawej strony:
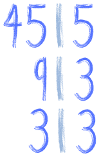
Wynik tego dzielenia znów zapiszemy z prawej strony:

I na tym koniec, bo jedynka dzieli się już tylko przez 1.
A więc dzielnikami liczby 45 są: 5, 3, 3 i 1. Tak, trójka pojawia się w tym zestawie dwa razy.
Jak rozłożyć na czynniki pierwsze liczbę 2 025?
Proste? No to teraz jeszcze większa liczba. Weźmy 2 025.
Przez co się owa liczba dzieli? Widać na pierwszy rzut oka, że na pewno przez 5:
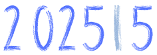
Ojć, ale ile to jest 2 025 podzielone przez 5? Jeśli nie jesteś w stanie policzyć w pamięci, możesz policzyć to sobie na boku w słupku. Nic nie stoi ku temu na przeszkodzie i nikt nie powinien ci na to zwracać uwagi.
Wiemy już zatem, że 2 025 : 5 = 405. 405 piszemy po lewej stronie:

Super. No ale nadal widzimy, że 405 też da się podzielić przez 5. Ile wychodzi? Jeśli 81, to dobrze policzyłeś. Zapiszmy:
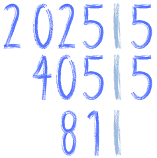
A 81 przez co? Bystrzachy powiedzą, że przez 9 i będą mieli rację :) My jednak chcemy mieć liczby pierwsze, więc pewnie powiemy, że przez 3:
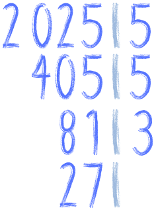
Wynik już zapisany, znów z prawej strony. A teraz już łatwo, bo 27 znów dzieli się przez 3, prawda?

Zostało 9, które znów nam się przez 3 ładnie dzieli. Zapiszmy:

No i trójka dzieli się przez siebie i przez 1:

Zostaje jeden, czyli kończymy tą przygodę. A więc dzielnikami liczby 2 025 są liczby: 5, 5, 3, 3, 3, 3 i 1.
Jak to zrobić szybciej?
A czy można skrócić sobie proces myślowy i zapisać od razu większe dzielniki? Na przekład tak:

Zależy do czego potrzebujesz wynik. Jeśli jest ci on potrzebny pośrednio przy liczeniu zadania (przykład znajdziesz poniżej), to tak. Ale jeśli treścią zadania jest rozłożenie owej liczby właśnie na czynniki pierwsze, to musimy wypisać wszystkie możliwe dzielniki owej liczby pojedynczo. Wtedy powyższy zapis nie będzie już prawidłowy.
Do czego się przyda rozłożenie liczby na czynniki pierwsze?
Na przykład gdy chcemy wyciągnąć pierwiastek z większej liczby, a nie możemy skorzystać z kalkulatora.
Jak obliczyć pierwiastek z 2 025?
Weźmy liczbę 2 025 z poprzedniego przykładu. Ile wynosi pierwiastek z 2 025? Niektórzy za głowę się złapią, no bo jak to policzyć bez kalkulatora?! Bardzo prosto ;)
Skoro

Albo

No to
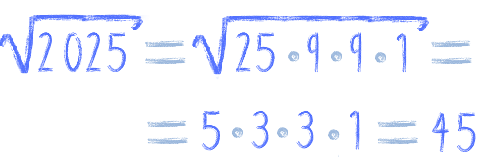
W tym przypadku można skorzystać właśnie z prostszego i szybszego zapisu, że

Za łatwe, Alicja, daj coś trudniejszego! Proszę bardzo. Oblicz pierwiastek z 1 089.
Obliczamy pierwiastek z 1 089
Rozkładamy sobie liczbę najpierw na czynniki pierwsze:
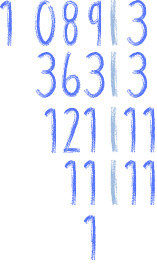
Albo od razu:

Jak widzisz wcale nie musimy pisać dzielników od największego. Możesz zacząć od tego dzielnika, który widzisz na pierwszy rzut oka albo od tego, który pierwszy przyjdzie ci do głowy.
No to skoro

to
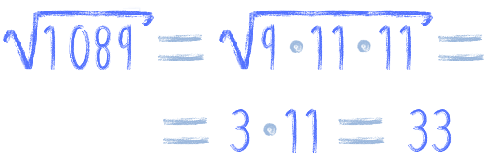
Wspólny mianownik
Rozkładanie liczby na czynniki pierwsze przyda się też gdy chcemy znaleźć wspólny mianownik dwóch ułamków. Zobacz takie działanie:

Ułamki możemy odjąć tylko wtedy, jeśli mają one taki sam mianownik, prawda? Czyli musimy znaleźć wspólny mianownik dla obu ułamków.
Na pierwszy rzut oka nie wygląda to zbyt sympatycznie… Większość osób pewnie znów chwyci się za głowę, albo powie, że się nie da. Albo próbowaliby mnożyć 63 przez 27. Trochę duża liczba do mnożenia bez kalkulatora. Dałoby się to zrobić, ale zajęłoby to sporo czasu.
A ty masz jakiś pomysł? :) Rozłóżmy sobie oba mianowniki na czynniki pierwsze
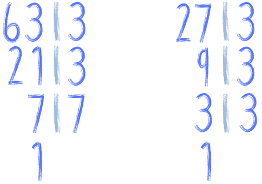
Aby dzielniki były takie same, w pierwszej liczbie brakuje jednej trójki, a w drugiej brakuje 7, prawda? Wystarczy więc rozszerzyć oba ułamki przez te dwie liczby aby mianowniki były takie same. Brzmi skomplikowanie? To zobacz:

Proste? jeśli tak, to super, jeśli nie to napisz proszę w komentarzu co jeszcze wytłumaczyć :)
A nie, no, jesli proste, to też napisz w komentarzu! Będzie mi miło :)
A teraz spróbuj sam rozłożyć na czynniki pierwsze takie liczby:
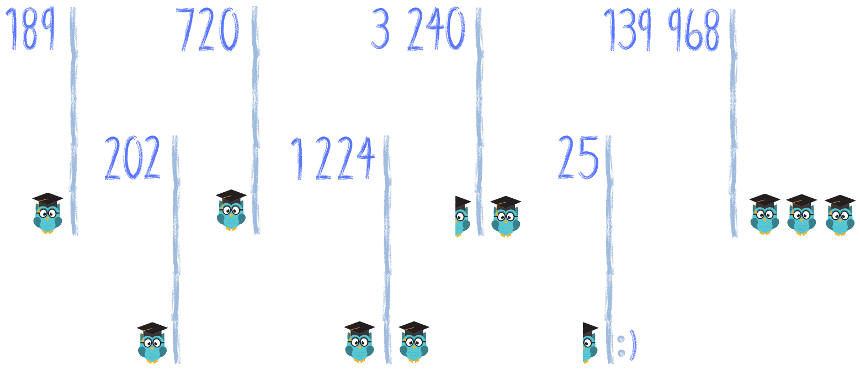
Za każde poprawnie rozwiązane zadanie zgarniasz tyle sów, ile siedzi przy zadaniu. Ile sów udało ci się zgarnąć? Pochwal się koniecznie w komentarzu! :)