Szczególnie gdy liczby są duże albo mało przyjemne. Bo wspólny mianownik dla takich ułamków znajdziemy raczej łatwo:

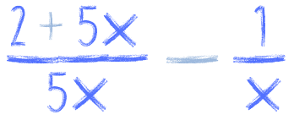
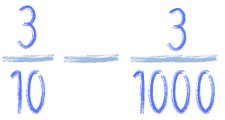
Spróbuj sam! Jeśli nie wiesz jak lub chcesz sprawdzić swój wynik, to rozwiązanie znajdziesz na końcu tej lekcji. Zaczekaj, najpierw spróbuj sam! ;)
Wspólny mianownik większych liczb
Ale co z takimi ułamkami:
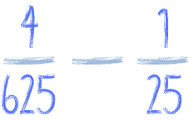
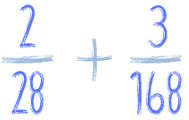
Gdy mamy w mianowniku duże liczby, które się nam nie podobają, to najlepiej rozłożyć sobie te liczby na czynniki pierwsze. Zobacz:
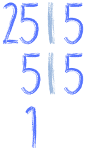

Co brakuje w liczbie 25 aby otrzymać 625? 25, prawda? Bo w 625 siedzą cztery piątki, a w 24 tylko dwie. Bo 25 * 25 = 625. A więc wystarczy drugi (odejmowany) ułamek rozszerzyć przez 25 i będziemy mieć wspólny mianownik. Napiszę to, będzie prościej:
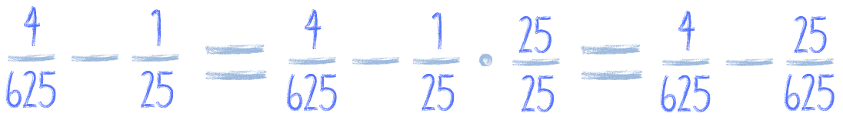
A skoro mamy wspólny mianownik, to można już odjąć ułamki :)
A co to znaczy rozserzyć ułamek przez liczbę? Aby to zrobić musimy ponożyć nasz ułamek przez drugi ułamek, który ma taką samą liczbę w liczniku i mianowniku. Bo ten drugi ułamek ma wartość 1, prawda? A więc jeśli nasz ułamek przemnożymy przez 1, to jego wartość się nie zmieni, a zmieni się nasz mianownik (licznik też owywiście, ale dla nas ma teraz znaczenie mianownik) na taki, który będzie taki sam jak mianownik drugiego ułamka, który chcemy do niego dodać lub odjąć. Brzmi jak jakaś straszna zamotka? To zobacz to na przykładach.
To było w miarę proste, prawda? Daj znać w komentarzu :)
Ale to drugie dodawanie już nie wygląda tak sympatycznie, no nie?
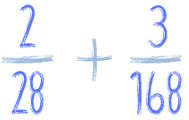
No to jedziemy, rozkładamy każdy mianownik na czynniki pierwsze:

I teraz drugi nasz mianownik tak samo:

A więc:

(jedynkę pomijamy, bo i tak nic ona do mnożenia nie wnosi).

Cóż więc za liczba brakuje nam w 28 aby mnożąc dostać 168? 6 prawda? A więc wystarczy rozszerzyć ułamek 2/28 o 6/6 aby otrzymać wspólny mianownik:
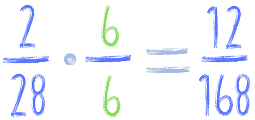
I teraz już możemy dodać oba ułamki:
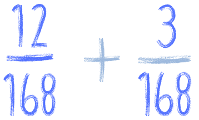
Być może ten sposób wydaje ci się w tej chwili dość skomplikowany, ale zobaczysz, że gdy przeliczysz więcej przykładów, zaczniesz znajdować wspólny mianownik o wiele szybciej. Bo na pierwszy rzut oka najprościej byłoby w powyższym przykładzie przemnożyć 28 * 168. Ale myślę, że nawet dwa proste działania 2 * 6 i 28 * 6 policzysz o wiele szybciej niż 28 * 168, a później jeszcze kolejne mnożenia, bo przecież:
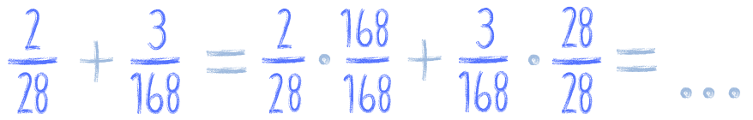
Tak szczerze to nie chce mi się nawet tego liczyć, bo wiem, że jest prostszy sposób, który pokazałam ci powyżej :)
Zadania dla ciebie :)
Spróbuj w ten sposób policzyć jeszcze kilka przykładów:
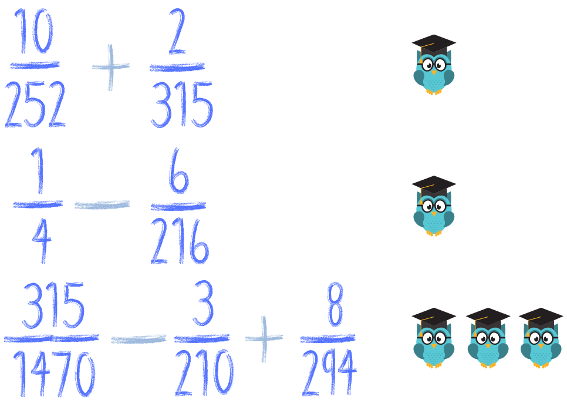
Za każde poprawnie rozwiązane zadanie zgarniasz tyle sów, ile siedzi przy zadaniu. Ile sów udało ci się zgarnąć? Pochwal się koniecznie w komentarzu! :)
Poprawne wyniki są na dole tej lekcji, ale zajrzyj tam dopiero, gdy sam zmierzysz się na spokojnie z zadaniami! :)
Rozwiązanie zadań z początku tej lekcji
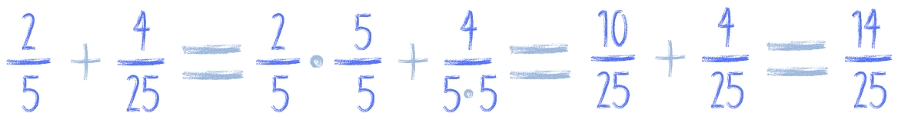
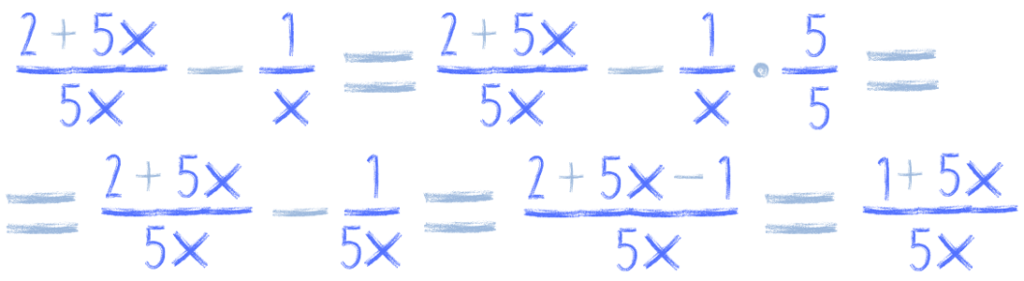

Wyniki zadań domowych

To ile sów masz w piórniku? Jeśli więcej niż dwie, to gratuluję! :) Jeśli mniej, to żadna tragedia, ale wyzwanie dla ciebie, aby jeszcze trochę poćwiczyć ten temat. Rozwiązując więcej zadań oczywiście!

