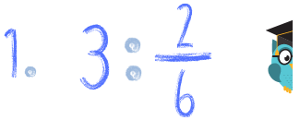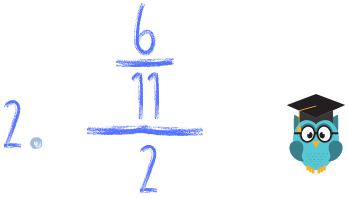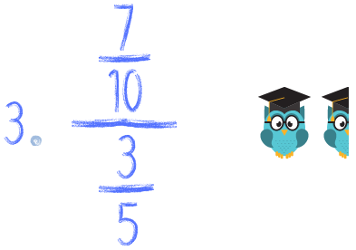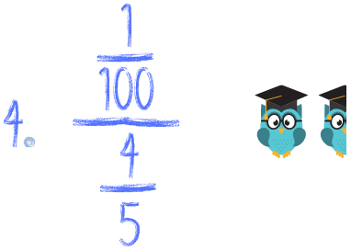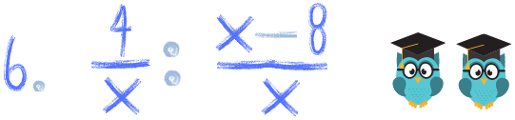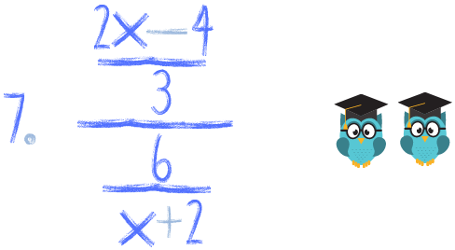Zdarza się, że zapominamy w zadaniach jak podzielić coś przez ułamek. Z jednym działaniem jeszcze jakoś sobie radzimy, ale jak mamy liczbę podzielić przez ułamek albo ułamek przez ułamek, to się robi problem.
Jak poradzić sobie z dzieleniem przez ułamek?
Dziś pokażę ci, jak sobie poradzić z dzieleniem przez ułamek, aby więcej takie działanie nie sprawiało problemów :)
To zacznijmy od początku. Co to znaczy podzielić coś przez ułamek? Wiesz? Dzielenie przez ułamek to nic innego jak mnożenie przez jego odwrotność. Pokażę ci to jak zawsze na przykładach, tak będzie prościej:

To jest w miarę proste, prawda?
Zauważ, że czasem mnożone ułamki można skrócić. Dlaczego warto to robić? Ano dlatego, że jeśli ułamki skrócimy, to zostaną nam do wymnożenia mniejsze liczby. Jeśli wymnozymy te większe liczby to oczywiście nic strasznego się nie stanie, ale po co sobie komplikować matematyczne życie? ;) A po drugie, nawet takie wymnożone duże liczby i tak na końcu będziemy musieli skrócić. Dlaczego? Bo żaden prawdziwy matematyk się nie ucieszy, gdy pokażesz mu jako wynik zadania nieskrócony ułamek…
Dzielenie liczby przez ułamek
Problemy zaczynają się właśnie, gdy pojawia się bardziej skomplikowane działanie, np. dzielenie liczby przez ułamek:

Takie działanie robimy dokładnie tak samo, jak przy dzieleniu ułamka przez ułamek. Czyli mnożymy przez odwrotność:
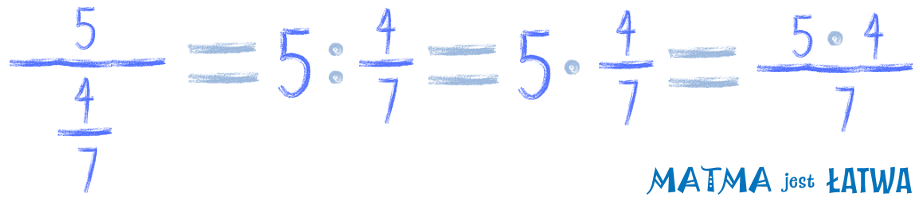
A później, gdy chcemy pomnożyć liczbę przez ułamek, mnożymy ją przez licznik (czyli to, co na górze) tego ułamka.
Dla ułatwienia można sobie napisać liczbę jako ułamek z jedynką w mianowniku, bo to przecież będzie nadal ta sama liczba, prawda?

I teraz już ładnie widać, co pomnożyć przez co. Licznik razy licznik i mianownik razy mianownik.
Zadanie dla ciebie: dokończ ostatni przykład i wpisz wynik w komentarzu! :)
Zwróć uwagę na kreskę ułamkową
Dobrym zwyczajem jest pisanie głównej kreski ułamkowej na wysokości znaku =. Wtedy o wiele ładniej widać co dzielimy przez co, niż gdybyś = napisał w jakimkolwiek miejscu. Zobacz jak jest bardziej czytelnie:

Bardziej skomplikowane ułamki
Tak samo dzielimy liczbę przez ułamek przy bardziej skomplikowanych ułamkach:
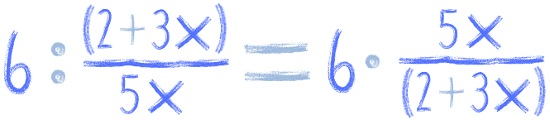
Przy mnożeniu zawsze liczbę 'wciągamy’ do licznika:
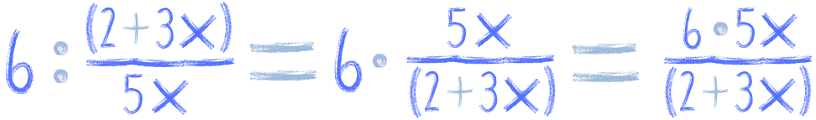
Zobacz jeszcze inne przykłady:
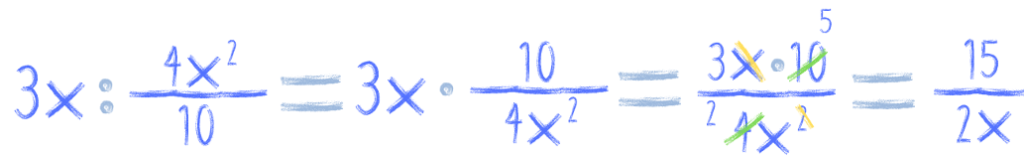
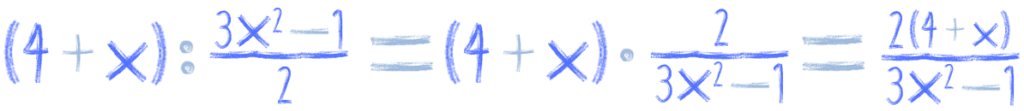

Ułamki piętrusy
Dość często zdarza się, że gdzieś w zadaniu pojawi się nam piętrus, jak nazywam ułamki takie:
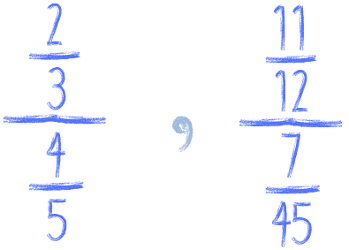
To nic innego jak po prostu dzielenie ułamka przez ułamek:
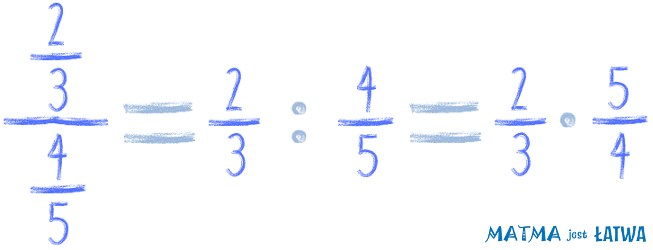
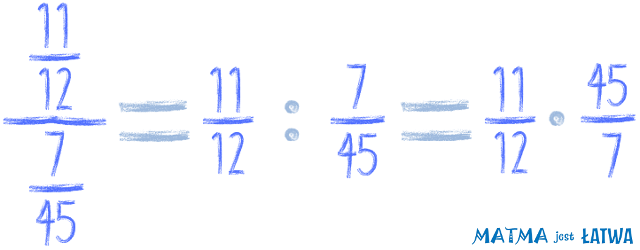
Zobacz zresztą na pierwszy przykład z tej lekcji. Równie dobrze możemy go zapisać w ten sposób:
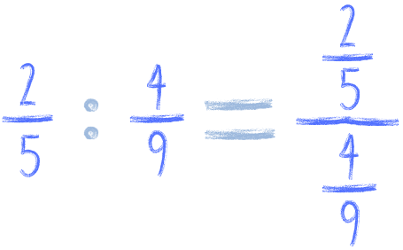
i też powstaje nam 'piękny’ ułamek piętrus.
Możemy mieć także dzielenie liczby przez ułamek zapisane jako piętrus:
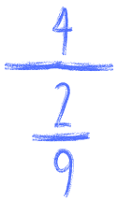
Albo dzielenie ułamka przez liczbę:
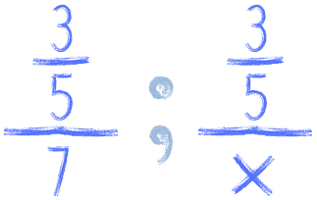
Wtedy robimy dokładnie to samo, co wyżej. Działania wykonujemy dokładnie tak, jak są zapisane, a więc dzielimy liczbę przez ułamek:
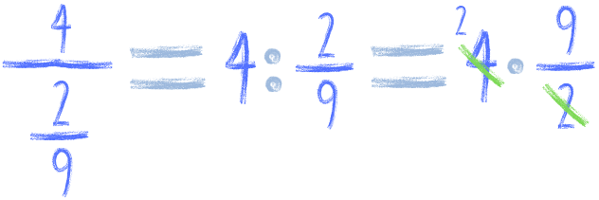
Albo dzielimy ułamek przez liczbę:
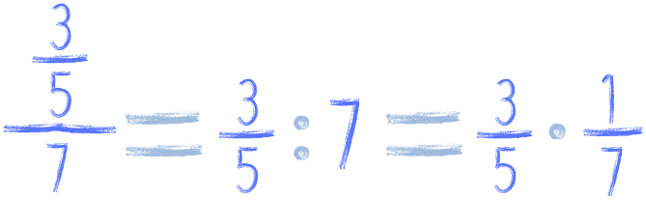
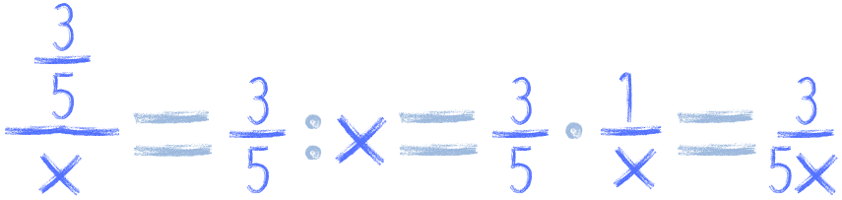
Nie jest to jakieś bardzo skomplikowane, prawda?
Wiem, że gorzej jest, gdy liczymy zdanie i pojawi się dzielenie przez ułamek. I tu sprawdza się nam znów stara zasada: im więcej zadań będziesz liczyć, tym łatwiej o takich dzieleniach przez ułamek będziesz pamiętał. Tym łatwiej będziesz je zauważał i przestaniesz się zastanawiać, jak to z tym dzieleniem ułamków było :)
Co może pójść nie tak?
Zdarza się, że niepoprawnie skracamy dzielenie piętrowych ułamków. Przykład? Proszę:

Tak jest źle, bo przecież:
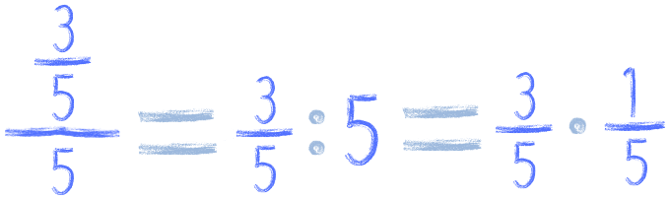
A tego skrócić się nie da, prawda?
Zobacz kolejny przykład:
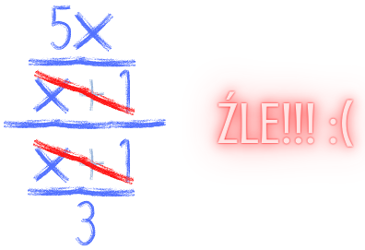
I znów tak nie powinniśmy robić, bo:
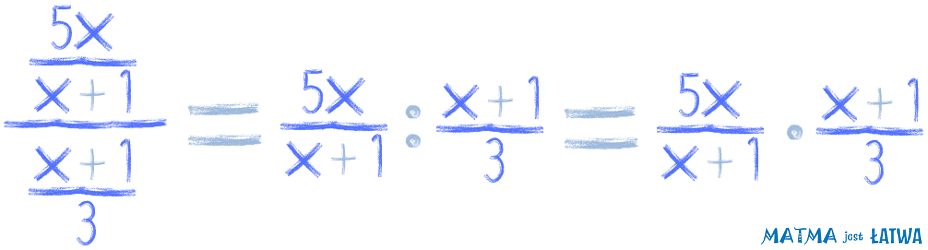
A później się dziwimy, że to zadanie coś zbyt skomplikowane jest. Albo że wynik się nie zgadza z odpowiedziami w teście.
Zawsze zatem zanim zaczniesz skracać takiego piętrusa, sprawdź dokładnie, czy na pewno możesz go skrócić. Bo zadania z matmy lubią być podchwytliwe :)
Zadania dla ciebie
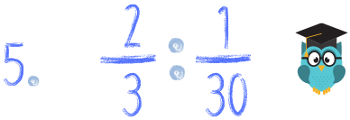
Spróbuj zrobić samodzielnie poniższe przykłady. Za każde poprawnie policzone zadanie zgarniasz tyle sów, ile przy nim siedzi. Pochwal się koniecznie w komentarzu ile sów zdobyłeś! :) A na koniec roku podsumujemy kto ma więcej :)